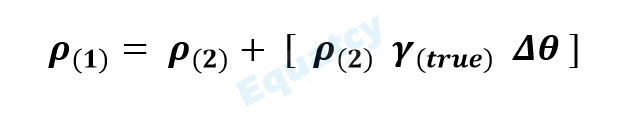01) Relationship between temperature scales
WHERE :
`C = Celsius scale
`F = Fahrenheit Scale
K = Kelvin scale
NOTE : Permanent low temperature is the value at which pure water becomes ice under standard atmospheric pressure ( o’ C , 32’ F , 273 K ) . Permanent high temperature is the value at which pure water becomes steam under standard atmospheric pressure ( 100’ C , 212’ F , 373 K ) .
©Equatcy
02) Triple point of water
WHERE :
T = Temperature required to measure (K)
x = Magnitude of the thermodynamic quality at the temperature required to measure
x(t) = Magnitude of the thermometric quality at the triple point
NOTE : The triple point of water is the temperature at which all the solid, liquid, and gaseous states are in equilibrium.
©Equatcy
03) Linear expansion of solids
WHERE :
ΔL = Difference in length
α = Linear expansion coefficient
L(1) = Startup length
L(2) = Last length
θ(1) = Temperature relative to the starting length
θ(2) = Temperature relative to the last length
NOTE: When an object is heat-increased and its temperature is increased relative to its length, these are called linear expansion.
©Equatcy
04) Area expansion of solids
WHERE :
ΔA = Difference in Area
β = Area expansion coefficient
A(1) = Startup Area
A(2) = Last Area
θ(1) = Temperature relative to the starting Area
θ(2) = Temperature relative to the last Area
NOTE: When an object is heat-increased and its temperature is increased relative to its Area, these are called Area expansion.
©Equatcy
05) Volume expansion of solids
WHERE :
ΔV = Difference in Volume
γ = Volume expansion coefficient
V(1) = Startup Volume
V(2) = Last Volume
θ(1) = Temperature relative to the starting Volume
θ(2) = Temperature relative to the last Volume
NOTE: When an object is heat-increased and its temperature is increased relative to its Volume, these are called Volume expansion.
©Equatcy
06) Relationship between expansion coefficients
WHERE :
α = Linear expansion coefficient
β = Area expansion coefficient
γ = Volume expansion coefficient
NOTE: Since the expansion coefficients are very small, the square is near to zero.
©Equatcy
07) Function of a bi-metal belt
WHERE :
R = Radius when changes temperature of the two-metal band
d(1) = Expansion large metal Thickness
d(2) = Expansion Small metal Thickness
α(1) = Expansion large metal coefficient
α(2) = Expansion Small metal coefficient
θ(1) = Lower temperature
θ(2) = High temperature
NOTE : Two different expansion coefficients of metals are arranged one by one for the operation of a two-metal band.
©Equatcy
08) Error in hanging clocks
WHERE :
T’ = Correct periodic period
T = Displayed periodic period
α = Expansion coefficient
ΔT = Periodic error
θ(1) = Lower temperature
θ(2) = High temperature
NOTE : A periodic clock can cause errors in the periodicity of the suspended clock depending on its temperature.
©Equatcy
09) True expansion of a liquid
WHERE :
∆V(true) = Total volume of the liquid increases
V(1) = First fluid volume
γ(true) = True liquid expansion coefficient
Δθ = Temperature difference
NOTE: True expansion is the full expansion of a liquid, taking into account the expansion of the pot.
©Equatcy
10) Visual expansion of a liquid
WHERE :
∆V(visual) = Volume of boiling liquid
V(1) = First fluid volume
γ(visual) = Visual liquid expansion coefficient
Δθ = Temperature difference
NOTE: It does not take into account the expansion of the pot.
©Equatcy
11) True total expansion of the liquid
WHERE :
∆V(True total) = True total expansion of the liquid
∆V(pot) = Expansion of the pot
∆V(visual) = Visual expansion of the liquid
NOTE: The volume expansion equation must be used to find the expansion of the pot.
©Equatcy
12) Relationship between temperature and density of a liquid
WHERE :
ρ(1) = Density at low temperature
ρ(2) = Density at high temperature
γ(true) = True expansion coefficient
∆θ = Temperature difference
NOTE: When heating a liquid, there is a decrease in the density and when the liquid is cooled the density increases.
©Equatcy
13) Heat capacity
C = m s
WHERE :
C = Heat capacity
m = Mass of the object
s = Specific Heat capacity of the object
NOTE: Heat capacity is the amount of heat that must be supplied or discharged to change the temperature of the object by 1 degree Celsius.
©Equatcy
14) Thermal energy ( which does not change the situation)
Q = C Δθ
Q = m s Δθ
WHERE :
Q = Thermal energy
C = Heat capacity
m = Mass of the object
s = Specific Heat capacity of the object
Δθ = Temperature difference
NOTE: Here solid, liquid, and gaseous phase does not change.
©Equatcy
15) Thermal energy (changes the situation)
Q = m L
WHERE :
Q = Thermal energy
L = Specific latent heat of evaporation
m = Mass that turned into steam
NOTE: Here solid, liquid, and gaseous phase change of matter.
©Equatcy
16) Heat transfer rate
WHERE :
Q / t = Heat transfer rate
L = Specific latent heat of evaporation
m = Mass that turned into steam
M = Mass of the object
s = Specific Heat capacity of the object
Δθ = Temperature difference
t = Time (කාලය)
NOTE: Here we consider how rapidly the temperature change or phase change occurs.
©Equatcy
17) Temperature gradient
WHERE :
G = Temperature gradient
Δθ = Temperature difference
l = Gap
NOTE: Temperature gradient is the temperature difference across units.
©Equatcy
18) Rate of Thermal conduction
WHERE :
Q/t = Rate of Thermal conduction
K = Thermal conductivity coefficient
A = Cross-sectional area of the conductor
l = Distance between the temperature measured points
Δθ = Difference between the temperatures
NOTE : Thermal conductivity coefficient is higher in conductors and lower in non-conductors.
©Equatcy
19) Density
WHERE :
V = Volume
ρ = Density
m = Mass
NOTE: As the volume increases, the density decreases.
©Equatcy
20) Newton's law of cooling
WHERE :
ΔQ/ Δt = Heat Damage Rate
E = Cooling constant
A = Cross-sectional area of Surface
θ = Temperature of the object
θ(r) = Temperature of the environment
NOTE : Newton's law of cooling can be applied to any temperature difference under artificial convection, but under natural convection the additional temperature is about 30 degrees Celsius.
©Equatcy
21) Cooling rate
WHERE :
Δθ/ Δt = Cooling rate
t = Time
θ(1)- θ(2) = Temperature drop
NOTE : As the heat dissipates from any object, its temperature decreases and the temperature drop per unit time is the cooling rate.
©Equatcy
22) Relation between cooling rate and Newton's law of cooling
WHERE :
Δθ/ Δt = Cooling rate
E = Cooling constant
A = Cross-sectional area of Surface
m = Mass of the object
s = Specific Heat capacity of the object
θ(r) = Temperature of the environment
θ = Temperature of the object
NOTE : Here is the relationship between the cooling temperature and the extra temperature of an object that is damaged by convection.
©Equatcy
23) Pressure
WHERE :
P = Pressure
cosθ = Angle to the surface
F = Force perpendicular to the surface
A = Surface area
NOTE: When pressure is measured always must use perpendicular force to the Surface.
©Equatcy
24) Boyle's law
WHERE :
P(1) = First case pressure
P(2) = Second stage pressure
V(1) = First case volume
V(2) = Second case volume
NOTE : The mass and temperature of the gas must be constant for any two instances of Boyle's law.
©Equatcy
25) Charles's law (type 1)
WHERE :
T(1) = First case Temperature
T(2) = Second stage Temperature
V(1) = First case volume
V(2) = Second case volume
NOTE : The mass and pressure of the gas must be constant for any two instances of Charles's law.
©Equatcy
26) Charles's law (type 2)
WHERE :
T(1) = First case Temperature
T(2) = Second stage Temperature
P(1) = First case Pressure
P(2) = Second case Pressure
NOTE : The mass and Volume of the gas must be constant for any two instances of Charles's law.
©Equatcy
27) Gas phase equation
WHERE :
T(1) = First case Temperature
T(2) = Second stage Temperature
P(1) = First case Pressure
P(2) = Second case Pressure
V(1) = First case Volume
V(2) = Second case Volume
NOTE : This equation is used for two stages of gas and in both cases the gas mass must be constant.
©Equatcy
28) Number of moles
WHERE :
n = Number of moles
m = Mass of the gas
M = Molecular mass
N = Number of subsets or atoms
L = Avogadro number
NOTE: This formula is used to find the number of moles.
©Equatcy
29) Perfect gas equation
P V = n R T
WHERE :
n = Number of moles
R = Universal gas constant
T = Temperature
P = Pressure
V = Volume
NOTE: Derivative equations can be obtained by substituting the appropriate formulas for the number of moles or the density of the gas. The universal air constant is 8.314 joules per mole per Kelvin.
©Equatcy
30) Boltzmann gas constant
WHERE :
K = Boltzmann gas constant
R = Universal gas constant
L = Avogadro number
NOTE: These equations are used to obtain derivative equations..
©Equatcy
31) Perfect gas equation with the Boltzmann gas constant
P V = n K T
WHERE :
n = Number of moles
K = Boltzmann gas constant
T = Temperature
P = Pressure
V = Volume
NOTE: Perfect gas equation is derived from the Boltzmann gas constant.
©Equatcy
32) Mass of a gas
WHERE :
m = Mass of a gas
N = Number of subsets or atoms
m``` = Mass of an subset or atom
NOTE: This equation is used to derive equations.
©Equatcy
33) Equation of kinetic theory
WHERE :
m``` = Mass of subsets
N = Number of subsets or atoms
C^2 = Root mean square velocity
P = Pressure
V = Volume In the gas
ρ = Density of the gas
m = Mass of a gas
NOTE : When a particle of gas moves in different directions in closed pot , the total momentum is zero.
©Equatcy
34) Kinetic energy of an air subset
WHERE :
E = Kinetic energy of an air subset
m``` = Mass of subsets
K = Boltzmann gas constant
C^2 = Root mean square velocity
T = Temperature
NOTE : Only kinetic energy of one air subset is obtained here.
©Equatcy
35) Total Kinetic energy of an air subset
WHERE :
E = Kinetic energy of an air subset
m``` = Mass of subsets
K = Boltzmann gas constant
C^2 = Root mean square velocity
T = Temperature
N = Number of subsets or atoms
NOTE : Total kinetic energy of air subsets are obtained here.
©Equatcy
36) Relationship between Root mean square velocity and temperature
WHERE :
R = Universal gas constant
C^2 = Root mean square velocity
T = Temperature
M = Molecular mass
NOTE : These equation is obtained by deriving the air equations.
©Equatcy
37) Heat exchanged in a thermodynamic system
WHERE :
∆Q = Heat exchanged difference in the system
∆u = Internal energy change in the system
∆W = Difference in the work done with the environment
NOTE: This law is the expression of the interplay of heat, internal energy, and work in a gas.
©Equatcy
38) Work done by the pressure of a gas
WHERE :
∆W = Work done by the pressure of a gas
P = Pressure
∆V = Volume difference
NOTE: It describes the work done by changing the volume of a gas-containing system.
©Equatcy
39) Relationship between molecular heat capacity
WHERE :
C(p) = Molecular heat capacity at constant pressure
C(v) = Molecular heat capacity at constant volume
R = Universal gas constant
γ = constant
NOTE: The difference between the molecular heat capacity is equal to the universal gas constant.The ratio between the molecular heat capacity of any gas is constant.
©Equatcy
40) Absolute humidity
WHERE :
A(r) = Absolute humidity
m(v) = Mass of vapor
V = Volume
NOTE: When a space is saturated with water vapor, the maximum absolute humidity is produced at that temperature.
©Equatcy
41) Relative humidity
WHERE :
R(h) = Relative humidity
m = Mass of vapor in a given volume at a given temperature
m(o) = Mass of water vapor required to saturate that volume at that temperature
NOTE : The lateral pressure is equal to the unsaturated vapor pressure.
©Equatcy
42) Relationship with relative humidity and pressure
WHERE :
R(h) = Relative humidity
P = Lateral pressure of water vapor at a given temperature
P(o) = Saturated vapor pressure at that temperature
NOTE : Humidity can be defined in terms of water vapor pressure.
©Equatcy