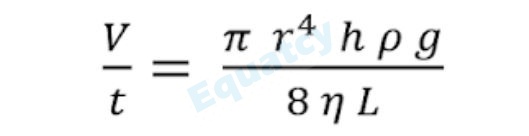1) Velocity gradient of viscosity
WHERE :
dV/dt = Velocity gradient of viscosity
V(1) - V(2) = Velocity difference
d = Gap
NOTE: Two different velocity of fluids and the gap is considered here.
©Equatcy
2) Newton's equation for viscosity
WHERE :
F = Viscous frictional force
V(1) - V(2) = Velocity difference
d = Gap
A = Contact area
η = Viscosity coefficient
NOTE: It is essential that the Fluid and object are in uniform motion.
©Equatcy
3) Upward thrust force
u = V ρ g
WHERE :
u = Upward thrust force
ρ = Density
g = Gravitational acceleration
NOTE: A force that depends on the volume and density of the object. A force acting against the weight of the object.
©Equatcy
4) Stoke's law of viscosity
WHERE :
F = Viscous resistance force
η = Viscosity coefficient
r = Radius of the sphere
V = The velocity of the sphere
NOTE: This equation is defined for sphere objects.
©Equatcy
5) Terminal velocity
WHERE :
V(0) = Terminal velocity
r = Radius of the object
g = Gravitational acceleration
d = Density of the object
ρ = Density of liquid
η = Viscous coefficient
NOTE: In a viscous fluid, an object that is freely abandoned moves at uniform velocity at a given some moment.
©Equatcy
6) Poisell equation of a cylindrical tube
WHERE :
V/t = Volume rate of Fluid
r = Radius of the object
η = Viscous coefficient
L = Length of the cylinder
P(1) – P(2) = Pressure difference
NOTE: This equation is used when the cylindrical tube is horizontal.
©Equatcy
7) Fluid pressure
P = h ρ g
WHERE :
P = Fluid pressure
ρ = Density
g = Gravitational acceleration
h = The height of the liquid beam
NOTE: The pressure of the liquid beam height is considered here.
©Equatcy
8) Poisell equation for liquid pressure
WHERE :
V/t = Volume rate of Fluid
r = Radius of the object
η = Viscous coefficient
L = Length of the cylinder
h = The height of the liquid stem
ρ = Density of liquid
g = Gravitational acceleration
NOTE: This equation is used when the liquid beam height and the cylindrical tube are horizontal.
©Equatcy
9) Poisell equation for a composite tube
WHERE :
V/t = Volume rate of Fluid
r(1) = Radius In the first tube
r(2) = Radius In the second tube
η = Viscous coefficient
L(1) = Length of the first cylinder
L(2) = Length of the second cylinder
P(1) - P(2) = Pressure difference
NOTE: The Volume rate of Fluid of two compact horizontal cylinders is considered here.
©Equatcy